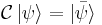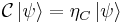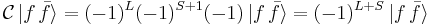C parity

In physics, C parity or charge parity is a multiplicative quantum number of some particles that describes its behavior under a symmetry operation of charge conjugation (see C-symmetry).

Charge conjugation changes the sign of all quantic charges (i.e., additive quantum numbers):

electrical charge
baryon number and lepton number
flavor charges: strangeness, charm, bottomness (formerly `beauty'), topness (formerly `truth')
Isospin 3rd-component

On the contrary, does not affect:

mass
linear momentum
spin J
complex conjugation K

As a result, a particle is substituted by its antiparticle.

$\mathcal C \, |\psi\rangle = | \bar{\psi} \rangle$

For the eigenstates of charge conjugation

$\mathcal C \, |\psi\rangle = \eta_C \, | \psi \rangle$

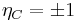and $\eta_C = \pm 1$ is called the C parity or charge parity.

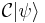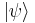The above implies that $\mathcal C|\psi\rangle$ and $|\psi\rangle$ have exactly the same quantum charges, so only truly neutral systems —those where all quantum charges and magnetic moment are 0— are eigenstates of charge parity, that is, the photon and particle-antiparticle bound states: neutral pion, η, positronium... The neutron is not an eigenstate because it has a magnetic moment, and so does not have an associated C parity.

For a system of free particles, the C parity is the product of C parities for each particle.

In a pair of bound bosons there is an additional component due to the orbital angular momentum. For example, in a bound state of two pions, π⁺ π⁻ with an orbital angular momentum L, exchanging π⁺ and π⁻ inverts the relative position vector, which is identical to a parity operation. Under this operation, the angular part of the spatial wave function contributes a phase factor of (−1)^L, where L is the angular momentum quantum number associated with L.

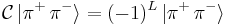$\mathcal C \, | \pi^%2B \, \pi^- \rangle = (-1)^L \, | \pi^%2B \, \pi^- \rangle$ .

With a two-fermion system, two extra factors appear: one comes from the spin part of the wave function, and the second from the exchange of a fermion by its antifermion.

$\mathcal C \, | f \, \bar f \rangle = (-1)^L (-1)^{S%2B1} (-1) \, | f \, \bar f \rangle = (-1)^{L %2B S} \, | f \, \bar f \rangle$

Bound states can be described with the spectroscopic notation ^2S+1L_J (see term symbol) , where S is the total spin quantum number, L the total orbital momentum quantum number and J the total angular momentum quantum number. Example: the positronium is a bound state electron-positron similar to an hydrogen atom. The parapositronium and ortopositronium correspond to the states ¹S₀ and ³S₁.

With S = 0 spins are anti-parallel, and with S = 1 they are parallel. This gives a multiplicity (2S+1) of 1 or 3, respectively
The total orbital angular momentum quantum number is L = 0 (S, in spectroscopic notation)
Total angular momentum quantum number is J = 0, 1
C parity η_C = (−1)^{L + S} = +1, −1, respectively. Since charge parity is preserved, annihilation of these states in photons (η_C(γ) = −1) must be:

	¹S₀	→	γ + γ		³S₁	→	γ + γ + γ
η_C:	+1	=	(−1) × (−1)		−1	=	(−1) × (−1) × (−1)

C parity

References

External links

See also